Path Sum

 Given the root of a binary tree and an integer targetSum, return true if the tree has a root-to-leaf path such that adding up all the values along the path equals targetSum.


A leaf is a node with no children.


 


Example 1:




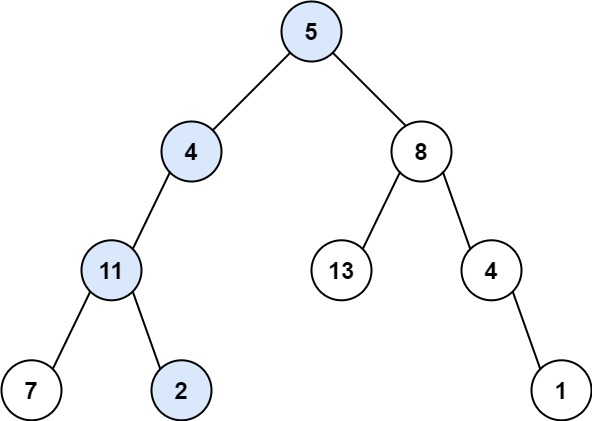
Input: root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22

Output: true

Explanation: The root-to-leaf path with the target sum is shown.

Example 2:



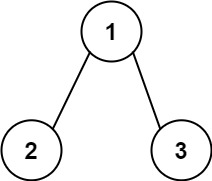
Input: root = [1,2,3], targetSum = 5

Output: false

Explanation: There are two root-to-leaf paths in the tree:

(1 --> 2): The sum is 3.

(1 --> 3): The sum is 4.

There is no root-to-leaf path with sum = 5.

Example 3:


Input: root = [], targetSum = 0

Output: false

Explanation: Since the tree is empty, there are no root-to-leaf paths.

 


Constraints:


The number of nodes in the tree is in the range [0, 5000].

-1000 <= Node.val <= 1000

-1000 <= targetSum <= 1000


🔄 Dry Run Step-by-Step (DFS Style):

Call: hasPathSum(5, 22)

  • Node = 5

  • Remaining = 22 - 5 = 17

Now explore both left and right:

▶ Left Subtree of 5: hasPathSum(4, 17)

  • Node = 4

  • Remaining = 17 - 4 = 13

▶ Left Subtree of 4: hasPathSum(11, 13)

  • Node = 11

  • Remaining = 13 - 11 = 2


→ Left Subtree of 11: hasPathSum(7, 2)

  • Node = 7 (leaf)

  • Check: 2 == 7? ❌

  • Return false

→ Right Subtree of 11: hasPathSum(2, 2)

  • Node = 2 (leaf)

  • Check: 2 == 2? 

  • Return true

Now we bubble up:
→ hasPathSum(11, 13) = true
→ hasPathSum(4, 17) = true
→ hasPathSum(5, 22) = true 

 How It "Decides" Path:

  • It tries all paths using recursion.

  • If any of them is valid, it returns true.

  • No path is “chosen” ahead — it's exploration via DFS.



/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
       
   if (root ==null) return false;
   if(isLeaf(root))
   {
   return  targetSum==root.val;
   }
 int remaianing=targetSum-root.val;
return hasPathSum(root.left,remaianing) || hasPathSum(root.right,remaianing);

    }

    public static boolean isLeaf(TreeNode root)
    {
        return (root.left==null) && (root.right==null);
    }
}

Comments

Post a Comment

Popular posts from this blog

Two Sum II - Input Array Is Sorted

 Given a 1-indexed array of integers numbers that is already sorted in non-decreasing order , find two numbers such that they add up to a specific target number. Let these two numbers be numbers[index1] and numbers[index2] where 1 <= index1 < index2 <= numbers.length. Return the indices of the two numbers, index1 and index2, added by one as an integer array [index1, index2] of length 2. The tests are generated such that there is exactly one solution. You may not use the same element twice. Your solution must use only constant extra space .   Example 1: Input: numbers = [2,7,11,15], target = 9 Output: [1,2] Explanation: The sum of 2 and 7 is 9. Therefore, index1 = 1, index2 = 2. We return [1, 2]. Example 2: Input: numbers = [2,3,4], target = 6 Output: [1,3] Explanation: The sum of 2 and 4 is 6. Therefore index1 = 1, index2 = 3. We return [1, 3]. Example 3: Input: numbers = [-1,0], target = -1 Output: [1,2] Explanation: The sum of -1 and 0 is -1. Therefore index1 = 1,...
Read more

Comparable Vs. Comparator in Java

  In Java , Comparable and Comparator both are interfaces used to sort objects. Comparable It defines  natural ordering  within a class. It is implemented  inside  the class being sorted. It uses the compareTo() method. It allows sorting  by one one . Comparable provides a  single sorting sequence . In other words, we can sort the collection on the basis of a single element such as id, name, and price. Comparable  affects the original class , i.e., the actual class is modified. Comparable is present in  java.lang  package. We can sort the list elements of Comparable type by  Collections.sort(List)  method. Only one compareTo() method can be implemented, restricting flexibility. Comparator It defines  custom sorting logic It is implemented  in a separate class  or using lambda expressions . It uses the compare() method. It allows sorting  by multiple criteria . The Comparator provides  multiple sorting...
Read more

Increasing Triplet Subsequence

 Given an integer array nums, return true if there exists a triple of indices (i, j, k) such that i < j < k and nums[i] < nums[j] < nums[k]. If no such indices exists, return false.   Example 1: Input: nums = [1,2,3,4,5] Output: true Explanation: Any triplet where i < j < k is valid. Example 2: Input: nums = [5,4,3,2,1] Output: false Explanation: No triplet exists. Example 3: Input: nums = [2,1,5,0,4,6] Output: true Explanation: The triplet (3, 4, 5) is valid because nums[3] == 0 < nums[4] == 4 < nums[5] == 6. Brute Force : Failed for some testcase class Solution {     public boolean increasingTriplet ( int [] nums ) {         int n = nums . length ;         int i = 0 ;         int j =i+ 1 ;         int k =j+ 1 ;         while (i <n && j<n && k<n)         {         if (nums...
Read more