Binary Tree Inorder Traversal -Left → Root → Right

 Given the root of a binary tree, return the inorder traversal of its nodes' values.


 


Example 1:


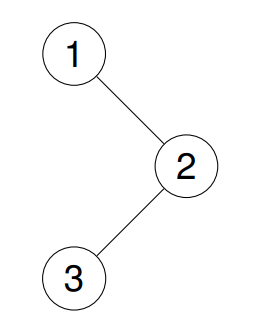
Input: root = [1,null,2,3]


Output: [1,3,2]


Explanation:



Example 2:


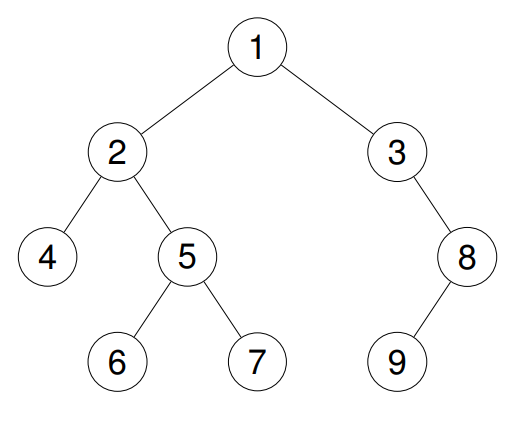
Input: root = [1,2,3,4,5,null,8,null,null,6,7,9]


Output: [4,2,6,5,7,1,3,9,8]


Explanation:



Example 3:


Input: root = []


Output: []


Example 4:


Input: root = [1]


Output: [1]


Approach 1: Recursive (Briefly)


/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
         List<Integer> result = new ArrayList<>();
        inorder(root, result);
        return result;
    }
    void inorder(TreeNode node,List<Integer> result) {
    if (node == null) return;

    inorder(node.left,result);     // 1. Traverse Left
   // System.out.print(node.val);  // 2. Visit Root
   result.add(node.val);
    inorder(node.right,result);    // 3. Traverse Right
}
}



Approach 2: Iterative (Important)

🔹 Why use a stack?

  • Because we need to go all the way left, and then come back to visit, and go right.

  • The stack remembers the path back up the tree.

🔹 Step-by-Step Algorithm:

  1. Initialize an empty stack.

  2. Initialize current = root.

  3. While current is not null or stack is not empty:

    • Go as far left as possible:

      • Push current to stack

      • Move current to left child

    • Once current is null:

      • Pop top node from stack

      • Visit (add to result)

      • Move to right child


class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        TreeNode current = root;

        while (current != null || !stack.isEmpty()) {
            // Step 1: Reach the leftmost node
            while (current != null) {
                stack.push(current);      // Save node
                current = current.left;   // Move to left
            }

            // Step 2: Process node
            current = stack.pop();        // Go back up
            result.add(current.val);      // Visit root

            // Step 3: Visit right child
            current = current.right;
        }

        return result;
    }
}

 

Comments

Post a Comment

Popular posts from this blog

Two Sum II - Input Array Is Sorted

 Given a 1-indexed array of integers numbers that is already sorted in non-decreasing order , find two numbers such that they add up to a specific target number. Let these two numbers be numbers[index1] and numbers[index2] where 1 <= index1 < index2 <= numbers.length. Return the indices of the two numbers, index1 and index2, added by one as an integer array [index1, index2] of length 2. The tests are generated such that there is exactly one solution. You may not use the same element twice. Your solution must use only constant extra space .   Example 1: Input: numbers = [2,7,11,15], target = 9 Output: [1,2] Explanation: The sum of 2 and 7 is 9. Therefore, index1 = 1, index2 = 2. We return [1, 2]. Example 2: Input: numbers = [2,3,4], target = 6 Output: [1,3] Explanation: The sum of 2 and 4 is 6. Therefore index1 = 1, index2 = 3. We return [1, 3]. Example 3: Input: numbers = [-1,0], target = -1 Output: [1,2] Explanation: The sum of -1 and 0 is -1. Therefore index1 = 1,...
Read more

Comparable Vs. Comparator in Java

  In Java , Comparable and Comparator both are interfaces used to sort objects. Comparable It defines  natural ordering  within a class. It is implemented  inside  the class being sorted. It uses the compareTo() method. It allows sorting  by one one . Comparable provides a  single sorting sequence . In other words, we can sort the collection on the basis of a single element such as id, name, and price. Comparable  affects the original class , i.e., the actual class is modified. Comparable is present in  java.lang  package. We can sort the list elements of Comparable type by  Collections.sort(List)  method. Only one compareTo() method can be implemented, restricting flexibility. Comparator It defines  custom sorting logic It is implemented  in a separate class  or using lambda expressions . It uses the compare() method. It allows sorting  by multiple criteria . The Comparator provides  multiple sorting...
Read more

Increasing Triplet Subsequence

 Given an integer array nums, return true if there exists a triple of indices (i, j, k) such that i < j < k and nums[i] < nums[j] < nums[k]. If no such indices exists, return false.   Example 1: Input: nums = [1,2,3,4,5] Output: true Explanation: Any triplet where i < j < k is valid. Example 2: Input: nums = [5,4,3,2,1] Output: false Explanation: No triplet exists. Example 3: Input: nums = [2,1,5,0,4,6] Output: true Explanation: The triplet (3, 4, 5) is valid because nums[3] == 0 < nums[4] == 4 < nums[5] == 6. Brute Force : Failed for some testcase class Solution {     public boolean increasingTriplet ( int [] nums ) {         int n = nums . length ;         int i = 0 ;         int j =i+ 1 ;         int k =j+ 1 ;         while (i <n && j<n && k<n)         {         if (nums...
Read more